Chemistry: Guide to NMR

NMR can only be conducted on atomic nuclei which have spins. These have either an odd mass number, odd atomic number, or both. The two introduced during A-level chemistry were H¹ and C¹³, undergrad level introduces others.

The number of spin states a nucleus may adopt is determined by its nuclear spin quantum number, I. There are 2I + 1 allowed spin states, with integral differences ranging from +I to -I.

For example, Cl³⁵ has I = 3/2. The range is from +I to -I, so from +3/2 to -3/2. Using integral differences, the allowed spin states are therefor 3/2, 1/2, -1/2, -3/2.

H¹ has an I = 1/2, and can adopt a spin state of +1/2 or -1/2, since a single integral difference bridges the gap from +I to -I.

A spinning charge generates a magnetic field of it's own, which points in different directions depending on the direction it spins in. This means the two states do not have equivalent energy when placed inside a magnetic field, since the magnetic fields generated by spinning nuclei could be aligned with the external field, or opposed.

One analogy used is a compass on earth with its needle pointing south. It will spontaneously flip to north if it can do so. To make the analogy better, imagine the energy of the compass is quantitized (for example, it can only point north or south with no intermediates). Also imagine that flipping from south to north will give off one single photon which is equal to the energy difference, and that it can absorb a proton to flip back to south.

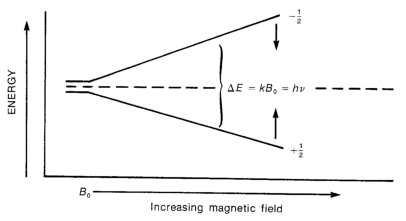
Splitting of the energy levels of a hydrogen nucleus spin states, as a magnetic force is applied

Just so the graph above doesn't deceive you: the energy levels change linearly with magnetic field strength they do not level off.

Here is the splitting of a Cl³⁵ nucleus:

Note the alignment diagram on the right. Using the compass analogy, it is like we are now given the choice to point northeast and southeast, in additional to north and south.

Here are two extra energy diagrams showing H¹ in a magnetic field.