Work and heat are both measured in joules, and are considered different ways of transferring energy. They are found experimentally to be easily intercovertable. Consider the pistons and cylinders below:
We can perform work on the left piston to compress it. Or heat the gas on the right to increase the pressure, pushing the piston, hence performing work. You could even use some of the work gained from the expanding gas to push current through a resistor, producing heat, and that heat can be used to expand a gas... and so on.
Work is the transfer of energy which makes use of ordered motion. The ordered direction of a falling piston introduces random kinetic motion into the gas molecules. So the piston is doing work which is converted to heating the gas.
Heat is the transfer of energy which makes use of random motion. The expansion of a gas in the cylinder will convert the random motion of gas particles into the ordered upwards motion of the piston. So heat from the gas is transformed into work.
The ordered and random motion does not have to be kinetic. An electric current is considered to move in an ordered motion, so using energy to drive a current would be considered doing work.
Pages
▼
van der Waal equation of state example
We simply multiple both sides by (Vm - b)Vm2 to get:
Then collect the powers of Vm to obtain:
Then plug the numbers into software to get a solution to this cubic equation.
van der Waals equation of state derivation
This attempts to account for some of the assumptions of the perfect gas equation of state. It is a good example of scientific thinking about a mathematical model, "model building" in other words. a and b are empirical parameters, but they can also be estimated.
First we take the ideal gas equation and try to account for volume taken up by the molecules themselves, by subtracting nb from the volume, where b is a constant.
This approximates molecules as hard spheres. So each molecule has a sphere of exclusion around it of 2r, anything less and the spheres would penetrated eachother.
This gives a total excluded volume of (4/3)π(2r)3 per molecule, which is 8Vmolecule.
This number is then halved "to prevent overcounting" to give 4Vmolecule. I have never been able to understand why this step is done.
But the end result is that b is roughly 4VNA. Since many molecules are quite soft, this number is typically the upper limit of empirical measurements.
The term on the right is because attractive forces will reduce both the rate of collisions of the molecules with the side of the container, and reduce the speed of these collisions. These forces are found to act with a strength proportional to the square of the molar concentration (n / V) of the molecules.
Remember that this is overwhelming an empirical law. And the justification given for it is only vague. There are other more satisfactory ones which you may come across later.
Real gases
A real gas approaches a perfect gas at 0 pressure. Attractive forces dominate at moderate pressures and repulsive forces at high pressure - since the repulsive forces have a shorter range.
Hence a real gas is expected to be more compressible at moderate pressures and less compressible at high pressures.
Compression factor
The compression factor is the ratio of the molar volume a gas compared to the molar volume of a perfect gas, at the same pressure and temperature:
From the equation you can see that Z of a perfect gas is 1. Real gases with a larger than perfect volume have Z > 1, and real gases with a lower than perfect volume have Z < 1.
From the argument in the first section we can expect Z to approach 1 and 0 pressure, be below 1 at moderate pressures, and above 1 at high pressure:
We can see this is true for most gases - H2 being a commonly-shown exception.
Partial pressures
In a mixture of gases, perfect or real, the partial pressure of an individual gas defined as:
pi = Patial pressure
p = Total pressure
xi = mole fraction of the gas
Note the following:
- Each mole fraction is between 1 and 0
- All the mole fractions in a mixture add up to one
- Total pressure is the sum of each partial pressure
These can also been understood intuitively by plugging in numbers.
If the gas is perfect, then Dalton's law applies:
pi = Patial pressure
p = Total pressure
xi = mole fraction of the gas
ni = moles of individual gas
n = total moles of all gases in the mixture
Note the following:
- Each mole fraction is between 1 and 0
- All the mole fractions in a mixture add up to one
- Total pressure is the sum of each partial pressure
These can also been understood intuitively by plugging in numbers.
If the gas is perfect, then Dalton's law applies:
The pressure exerted by a mixture of gases is the sum of the pressures that each one
would exist if it occupied the container alone.
Measuring pressure
A device to measure pressure is called a manometer. A device which measures atmospheric pressure is called a barometer. The simplest design for these is a column of mercury in a beaker:
When the atmospheric pressure is increase, force is applied on the mercury, pushing it up the column. Mechanical equilibrium is reached when this force is balanced by both increased pressure inside the column, and weight of the mercury inside the column.
If the column contains a vacuum, then the increased atmospheric pressure is balanced purely by the weight of the mercury.
Pressure is force divided by area. The weight of the lifted mercury is mg, so the pressure on the base of the column is this weight divided by cross-sectional area. This has to match the increase in atmospheric pressure for the system to be at equilibrium:
Pressure = mg / A
Since mass is volume*density:
Notice that pressure is independent of the cross-sectional area of the cylinder.
A more advanced solution is to use a curved tube:
The change in pressure is directly proportional to the difference in height of the two columns. A different of 1 mm corresponds to 1 mm Hg, also known as one torr.
The reason mercury is used is because of its low vapor pressure. Using a liquid like water would mean having to account for more vapor pressure in the sealed part of the tube - but it can be done.
When the atmospheric pressure is increase, force is applied on the mercury, pushing it up the column. Mechanical equilibrium is reached when this force is balanced by both increased pressure inside the column, and weight of the mercury inside the column.
If the column contains a vacuum, then the increased atmospheric pressure is balanced purely by the weight of the mercury.
Pressure is force divided by area. The weight of the lifted mercury is mg, so the pressure on the base of the column is this weight divided by cross-sectional area. This has to match the increase in atmospheric pressure for the system to be at equilibrium:
Pressure = mg / A
Since mass is volume*density:
Notice that pressure is independent of the cross-sectional area of the cylinder.
A more advanced solution is to use a curved tube:
The change in pressure is directly proportional to the difference in height of the two columns. A different of 1 mm corresponds to 1 mm Hg, also known as one torr.
The reason mercury is used is because of its low vapor pressure. Using a liquid like water would mean having to account for more vapor pressure in the sealed part of the tube - but it can be done.
Ethylene glycol
One of the most common acetal formation reactions you see in organic synthesis is the use of ethylene glycol. It is widely used as automotive antifreeze. A sweet-tasting, colorless, odourless liquid, which will kill pets or humans if they drink enough of it.
The TsOH is para-Toluenesulfonic acid. It is as strong as sulphuric acid, but exists as a stable white solid which makes it convenient to use. It is also non-oxidizing. And it dissolves in organic solvents.
Mechanism:
The TsOH is para-Toluenesulfonic acid. It is as strong as sulphuric acid, but exists as a stable white solid which makes it convenient to use. It is also non-oxidizing. And it dissolves in organic solvents.
Mechanism:
Don't miss out the formation of the oxonium ion.
A five-membered cyclic acetal is known as a dioxolane, as created in this example.
This forms readily even from ketones. 6-ring diols work too. I don't know why ethylene glycol is more common, presumably it is cheaper to make.
An example of the use of this protecting group is below:
The reaction works if we first protect the carbonyl. Since acetals are stable to a base (cyclic acetals moreso), the grignard reagent will only attack the Br. Once we have used the Grignard reagent to attack an electrophile, we can then hydrolyse the acetal off using acid and water.
Notice that water needs to be distilled off for the protecting group to be fully added. Thankfully, ethylene glycol has a boiling point of 197 C. If the reactants or solvent had a boiling point lower than water, then we could remove water using a Dean Stark Head with benzene.
Guide to symmetry
Symmetry symbols are a way to describe different shapes, molecules in our case, by categorizing them based on mathmatical properties, such as how many mirror planes a shape has. You've already seen two of them, sigma-symmetry ("cylindrical symmetry around the internuclear axis") and pi symmetry ("above and below").
In certain specialist fields such as crystallography, learning these notations can be really useful. For most chemistry undergraduates these are boring and without much use. But you will be tested on them. You are also likely to come across one or two annoying teachers who describe the shapes of molecules by symmetry notation, even when words like "octahedral" or "tetrahedral" refer to the same thing.
Symmetry operation: An action, such as rotation through a certain angle, which leaves the molecule apparently unchanged.
Symmetry element: A point, line, or plane, in which the symmetry operation is performed in respect to.
Different symmetry operations are described below.
Example, the rotation of H2O:
It involves rotation around a n-fold axis followed by reflection in the plane perpendicular to that axis:
In certain specialist fields such as crystallography, learning these notations can be really useful. For most chemistry undergraduates these are boring and without much use. But you will be tested on them. You are also likely to come across one or two annoying teachers who describe the shapes of molecules by symmetry notation, even when words like "octahedral" or "tetrahedral" refer to the same thing.
Symmetry operation: An action, such as rotation through a certain angle, which leaves the molecule apparently unchanged.
Symmetry element: A point, line, or plane, in which the symmetry operation is performed in respect to.
Different symmetry operations are described below.
N-fold rotation (Cn)
Example, the rotation of H2O:
The symmetry operation above is rotation of 180°. The symmetry element is the vertical line through the center of the molecule, called the n-fold rotational axis.
As you can see, the molecule is apparently unchanged. The central atom is considered not to be moved at all. All symmetry operations leave at least one point unmoved (the center of the molecule) which is why they are sometimes called operations of point group symmetry.
The C2 symbol in the diagram is an example of an n-fold rotation symmetry operation, with the general formula Cn. This is an operation if the molecule appears unchanged after rotation by 360 / n degrees. So you can find n by dividing 360° by the angle the structure must be rotated. Easiest way to understand it is by diagrams:
The subscript describes the angle, the superscript describes how many rotations of that angle are done in the symmetry operation.
Many molecules have multiple n-fold rotational axes which exams will ask you to spot. Xenon tetrafluroride for example:
By convention, the highest order n-fold axis is set as the Z axis, and is typically drawn vertically.
You might reason that C1, C22, C33, and many others are all symmetry operations. This is correct. But there is no point mentioning them since anything rotated by 360 degrees is symmetrical, so writing it doesn't help us distinguish the molecule.
The one exception to this attitude is the next operation:
Identity operation (E)
This consists of doing nothing to the molecule. They all have at least this operation, and some have only this operation.
I don't know why people go through the effort of writing this. I doubt many undergrads know either. But it is important because many exams will ask you to describe symmetry elements in a molecule, and simply writing "E" can get you a mark.
My textbook describes the symmetry element of E as being "the whole of space". Presumably there is mathematical justification for that.
Reflection (σ)
This operation simply describes mirror planes, denoted with a sigma symbol σ. Water has two σv planes:
This can be shown well with an octahedral shape:
In this case, the shape would only have inversion symmetry if all atoms were the same, or if 1 6, 3 and 5, 6 and 1, were equal to eachother. Tetrahedral shapes never have inversion symmetry.
Below is an ethene-shaped molecule, inversion is compared with a 2-fold rotation:
The subscript v or h refers to whether the planes are vertical or horizontal in respect to the principle axis of rotation - the axis with the highest number of turns.
For XeF4:
The d in σd means "dihedral", refering to the fact that it intercepts two axes of rotation. Presumably this is just a way to distinguish it from σd - the plane which intercepts fluorine atoms.
Inversion (i)
To see this we imagine a point in the molecule, move it towards the center of the molecule, then move it outwards from the center the same distance. If the molecule appears unchanged at all points, it contains i symmetry.This can be shown well with an octahedral shape:
In this case, the shape would only have inversion symmetry if all atoms were the same, or if 1 6, 3 and 5, 6 and 1, were equal to eachother. Tetrahedral shapes never have inversion symmetry.
Below is an ethene-shaped molecule, inversion is compared with a 2-fold rotation:
Improper rotation (S)
This is the most difficult to learn and to relearn, and probably often skipped in an exam question asking you to identify symmetry elements.It involves rotation around a n-fold axis followed by reflection in the plane perpendicular to that axis:
The example above uses a 90 degrees rotation - equivalent to a 4-fold axis, so we denote this in subscript as S4
A rotation of 360 degrees followed by reflection is equivalent to reflection alone, so we do not bother using S1 since we can use σ.
A rotation of 180 followed by reflection is equivalent to inversion. So we do not use S2 either, since we can use i.
Kinetics
A chemical reaction proceeds if the change in Gibbs energy is negative. But what determines how fast the reaction happens?
The answer depends on the mechanism. For example:
The mechanism here is just a proton colliding with a water molecule. So can predict intuitively that the reaction rate is proportional to the concentrations of each component, because higher concentrations increase the chance of a collision. Experiments confirm this model.
Not everyone collision results in a reaction. It needs to collide fast enough and at the right angle, for example the proton needs to collide with the oxygen atom in water. These effects are represented by a rate constant k.
Above is a gas phase example, but many reactions in solvents behave similarly, such as protonation of water by HCL:
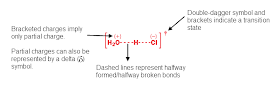
The reason the collision has to be fast enough is to overcome the activation energy - the energy of the transition state, which is when the new bond is partially formed and the old one is partially broken:
Transition states are just energy maxima, they cannot be isolated because any change in the structure pushes it towards a lower energy state. It would be like balancing a marble on top of a football, without friction.
The rate constant is also the part which varies with temperature.
The rate constant can be related to temperature and the activation energy of the reaction using the Eyring equation:











.gif)